Variational Gaussian processes for linear inverse problems
Abstract
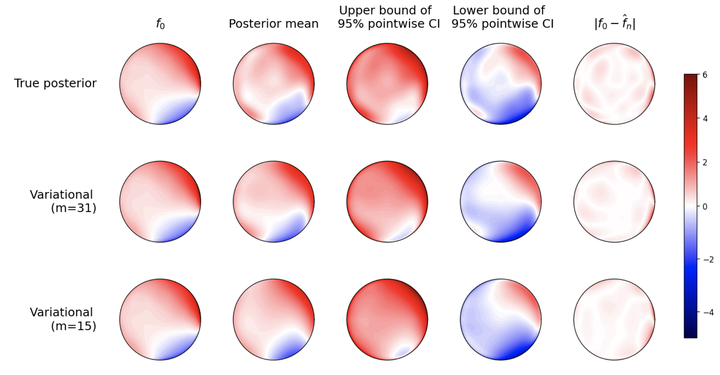
By now Bayesian methods are routinely used in practice for solving inverse problems. In inverse problems the parameter or signal of interest is observed only indirectly, as an image of a given map, and the observations are typically further corrupted with noise. Bayes offers a natural way to regularize these problems via the prior distribution and provides a probabilistic solution, quantifying the remaining uncertainty in the problem. However, the computational costs of standard, sampling based Bayesian approaches can be overly large in such complex models. Therefore, in practice variational Bayes is becoming increasingly popular. Nevertheless, the theoretical understanding of these methods is still relatively limited, especially in context of inverse problems. In our analysis we investigate variational Bayesian methods for Gaussian process priors to solve linear inverse problems. We consider both mildly and severely ill-posed inverse problems and work with the popular inducing variable variational Bayes approach proposed by Titsias [Titsias, 2009]. We derive posterior contraction rates for the variational posterior in general settings and show that the minimax estimation rate can be attained by correctly tunned procedures. As specific examples we consider a collection of inverse problems including the heat equation, Volterra operator and Radon transform and inducing variable methods based on population and empirical spectral features.